Here we will learn how to use SOHCAHTOA and trigonometry to find unknown sides and angles in right angled triangles. You’ll learn how to label the sides of right-angled triangles, what sin, cos and tan are, what their inverses are ( sin -1 , cos -1 , tan -1 ) and how we can use them.
Look out for the trigonometry practice problems, worksheets and exam questions at the end.
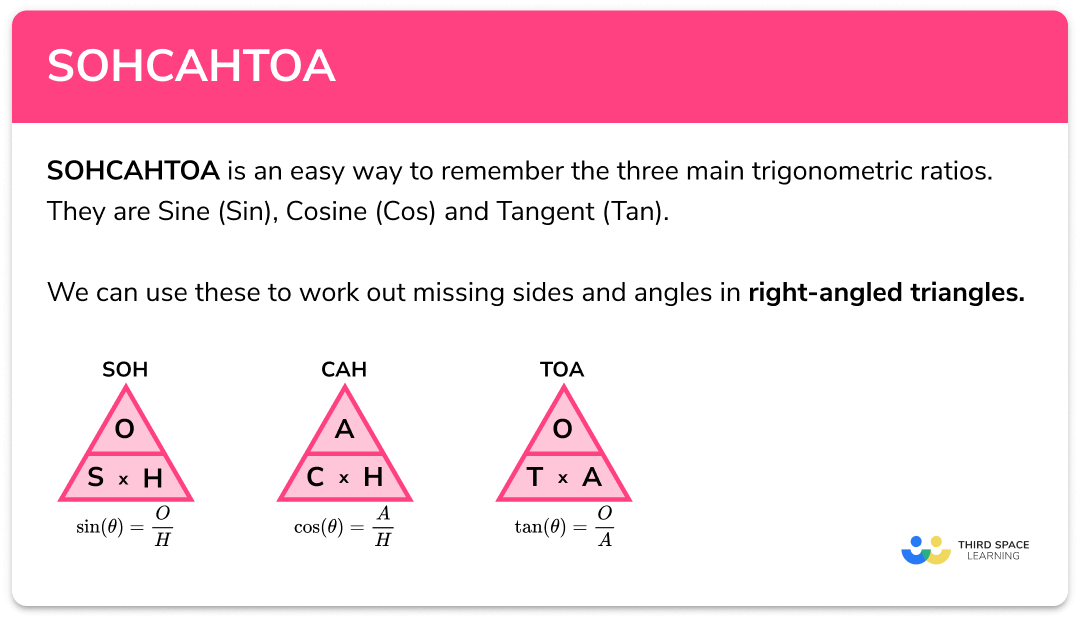
SOHCAHTOA is a mnemonic that gives us an easy way to remember the three main trigonometric ratios. They are sine ( sin ), cosine ( cos ) and tangent ( tan ).
We can use these to work out missing sides and angles in right-angled triangles.

We can abbreviate these to the SOHCAHTOA triangles:
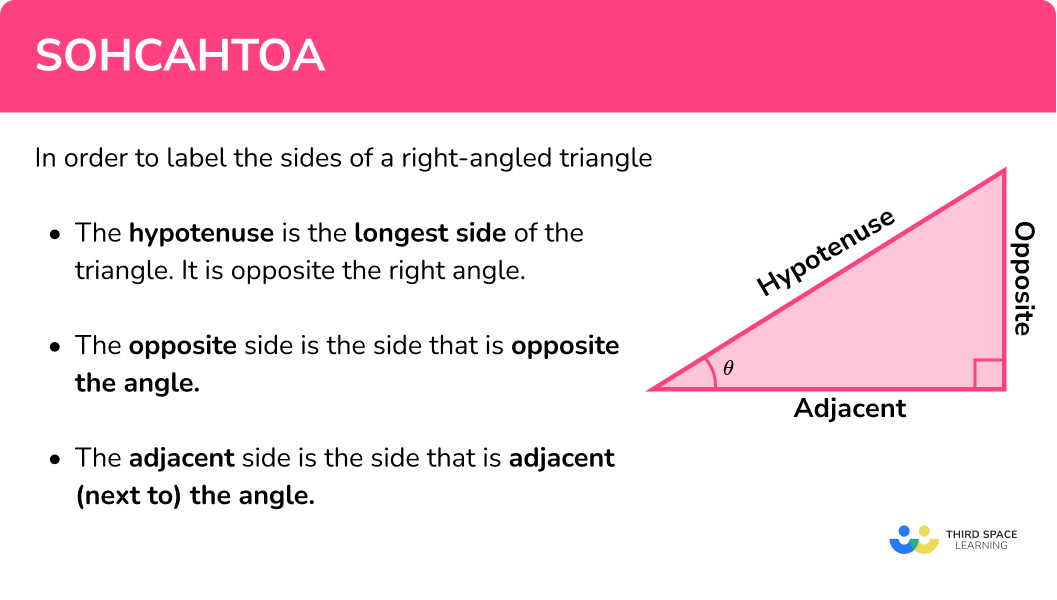
The hypotenuse is the longest side of the triangle. It is opposite the right angle.
The opposite side is the side that is opposite the angle.
The adjacent side is the side that is adjacent (next to) the angle.
E.g.
We have a right-angled triangle with a side of length 8 cm and a side of length x cm
Label the sides of the right-angled triangle.
2 Label the side opposite the angle O (opposite)
3 Label the side next to the angle A (adjacent)
Top tip: once you have labeled the hypotenuse (H) and the opposite (O), the adjacent (A) must be the only side left!
We can use trigonometry to work out the unknown sides of a right-angled triangle by using SOHCAHTOA.

Get your free SOHCAHTOA worksheet of 20+ questions and answers. Includes reasoning and applied questions.


Get your free SOHCAHTOA worksheet of 20+ questions and answers. Includes reasoning and applied questions.
Calculate the side labeled x
2 Choose the trig ratio we need.
The trigonometric function that involves the opposite (O) and the hypotenuse (H) is sin .
\[\sin(\theta)= \frac3 Substitute the values from the triangle into the function.
\[\sin(40)= \frac4 Calculate the unknown side, rearranging if necessary. We can either solve the equation or use the SOHCAHTOA triangles.
Always check that the answer is sensible:
As 5.1 is smaller than the 8 (the hypotenuse) it is a sensible answer.
Calculate the side labeled x
Label the sides of the right-angled triangle that we have information about.
Circle the labels so not to confuse them with the side lengths.
Choose the trig ratio we need.
The trigonometric function that involves the adjacent (A) and the hypotenuse (H) is cos .
\[\cos(\theta) = \fracSubstitute the values from the triangle into the function.
\[\cos(36) = \fracCalculate the unknown side, rearranging if necessary.
We can either solve the equation or use the SOHCAHTOA triangles.
Always check that the answer is sensible:
As 12.1 is smaller than the 15 (the hypotenuse) it is a sensible answer.
Calculate the side labeled x
Label the sides of the right-angled triangle that we have information about.
Circle the labels so not to confuse them with the side lengths.
Choose the trig ratio we need.
The trigonometric function that involves the opposite (O) and the adjacent (A) is tan .
\[\tan(\theta) = \fracSubstitute the values from the triangle into the function.
\[\tan(36) = \frac<10>\]Calculate the unknown side, rearranging if necessary.
We can either solve the equation or use the SOHCAHTOA triangles.
Always check that the answer is sensible:
A good sketch tells us this answer looks reasonable.
1. Calculate the length of the side labeled x . Give your answer to 1 d.p.




Label the triangle:
We know H and we want to work out O so use sin .
\begin \sin(\theta)&=\frac\\ \sin(23)&=\frac\\ 20 \times \sin(23) &= x\\ 7.81462257 &= x\\ x&=7.8\mathrm \end
2. Calculate the length of the side labeled x . Give your answer to 2 d.p.




Label the triangle:
We know A and we want to find H so use cos .
3. Calculate the length of the side labeled x . Give your answer to 2 s.f.




Label the triangle:
We know O and we want to work out A so use tan .
In order to work out missing angles in right-angled triangles we need use the inverse trigonometric functions:
\[\sin ^ <-1>\qquad \cos ^ <-1>\qquad \tan ^<-1>\]We can find these on the calculator by pressing SHIFT and then sin , cos or tan .
Step by step guide: Inverse trigonometric functions (coming soon)
We can use trigonometry to work out the unknown angles of a right-angled triangle by using SOHCAHTOA.
Calculate the angle labeled θ.
Label the sides of the right-angled triangle that we have information about.
Choose the trig ratio we need.
The trigonometric function that involves the opposite (O) and the hypotenuse (H) is sin .
\[\sin(\theta) = \fracSubstitute the values from the triangle into the function.
\[\sin(\theta) = \frac<5>\]Using inverse trig functions, work out the missing angle θ.
Remember we can get sin -1 on the calculator by pressing SHIFT and then sin .
Always check that the answer is sensible: We can estimate from the diagram that θ is an acute angle.
As 33.7 o is less than 90 o it is a sensible answer.
Calculate the angle labeled θ.
Label the sides of the right-angled triangle that we have information about.
Choose the trig ratio we need.
The trigonometric function that involves the adjacent (A) and the hypotenuse (H) is cos .
\[\cos(\theta) = \fracSubstitute the values from the triangle into the function.
\[\cos(\theta) = \frac<9>\]Using inverse trig functions, work out the missing angle θ.
Remember we can get cos -1 on the calculator by pressing SHIFT and then cos .
Always check that the answer is sensible: We can estimate from the diagram that θ is an acute angle.
As 63.7 o is less than 90 o it is a sensible answer.
Calculate the angle labeled θ.
Label the sides of the right-angled triangle that we have information about.
Choose the trig ratio we need.
The trigonometric function that involves the opposite (O) and the adjacent (A) is tan .
\[\tan(\theta) = \fracSubstitute the values from the triangle into the function.
\[\tan(\theta) = \frac<15>\]Using inverse trig functions, work out the missing angle θ.
Remember we can get tan -1 on the calculator by pressing SHIFT and then tan .
Always check that the answer is sensible: We can estimate from the diagram that θ is an acute angle.
As 65 o is less than 90 o it is a sensible answer.
We can use SOHCAHTOA to find a missing angle of a right angled triangle when we have two given sides.
SOHCAHTOA is part of our series of lessons to support revision on trigonometry. You may find it helpful to start with the main trigonometry lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
1. Calculate the size of the angle labeled \theta . Give your answer to 3 s.f.




Label the triangle:
We know O and H so use sin .
2. Calculate the size of the angle labeled \theta . Give your answer to 2 s.f.




Label the triangle:
We know A and H so use cos .
3. Calculate the size of the angle labeled \theta . Give your answer to 1 d.p.




Label the triangle:
We know O and A so use tan .
1. Find the size of angle a to 2.d.p.
(3 marks)
Show answer(1)
(1)
(1)
2. Rosie is flying a kite. She holds the kite string 1m from the ground. The kite string is 10m long and the kite flies at an angle of 40^ . Calculate the height of the kite above the ground.
(3 marks)
Show answer \begin \sin(40)&=\frac\\ 10\sin(40)&=opp \end(1)
(1)
(1)
3. Length AB = 15cm
Work out the length of DE .
(4 marks)
Show answer(1)
(1)
(1)
(1)
You have now learned how to:
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

© 2024 Third Space Learning. All rights reserved.
Third Space Learning is the trading name of Virtual Class Ltd
We use essential and non-essential cookies to improve the experience on our website. Please read our Cookies Policy for information on how we use cookies and how to manage or change your cookie settings.Accept
Privacy & Cookies PolicyThis website uses cookies to improve your experience while you navigate through the website. Out of these, the cookies that are categorized as necessary are stored on your browser as they are essential for the working of basic functionalities of the website. We also use third-party cookies that help us analyze and understand how you use this website. These cookies will be stored in your browser only with your consent. You also have the option to opt-out of these cookies. But opting out of some of these cookies may affect your browsing experience.
Always EnabledNecessary cookies are absolutely essential for the website to function properly. This category only includes cookies that ensures basic functionalities and security features of the website. These cookies do not store any personal information.
Non-necessaryAny cookies that may not be particularly necessary for the website to function and is used specifically to collect user personal data via analytics, ads, other embedded contents are termed as non-necessary cookies. It is mandatory to procure user consent prior to running these cookies on your website.